1 Reference manual
1.1 Operations on forests
Forests are ordered collections of unranked trees over some alphabet. Concatenation of forests (putting a forest after another) is denoted additively (although it is not a commutative operation) while the a-rooting of a forest f (the tree of root a and having f as children) is denoted multiplicatively.
1.1-1 Forest
> Forest( Expression ) | ( function ) |
Creates a forest object. Expression can either be a string containing the decomposition of the forest into sums and rootings, following this syntax:
Forest ::= a | Forest+Forest | a(Forest)
or it can use the internal list representation; labels are lower case characters, e.g. 'a', rootings are stored in list in which the first value is the label of the rooting node and the second is the list describing the rooted forest. Finally, the sum of two forests is the concatenation of the list that describe them
gap> f := Forest("a+b(a(b)+b(a+a))+c(c(c+a)+b)");
a+b(a(b)+b(a+a))+c(c(c+a)+b)
gap> g := Forest(['b', ['a',['b','b']]]);
b+a(b+b)
|
1.1-2 \+
> \+( Forest1, Forest2 ) | ( function ) |
Returns the concatenation of Forest1 and Forest2 into a new forest;
gap> f+g;
a+b(a(b)+b(a+a))+c(c(c+a)+b)+b+a(b+b)
|
1.1-3 ForestRooting
> ForestRooting( Char, Forest ) | ( function ) |
Returns the rooting of Forest under the lowercase character Char.
gap> ForestRooting('b', f);
b(a+b(a(b)+b(a+a))+c(c(c+a)+b))
|
1.1-4 WriteDotForest
> WriteDotForest( Forest, File ) | ( function ) |
This will convert the forest Forest into a DOT graph file for the GraphViz library. File is the name of the output file, this function returns the temporary directory where the DOT file was written.
gap> WriteDotForest(f, "forest.dot");
dir("/tmp/tmp.sGATtd/")
|
1.1-5 DrawForest
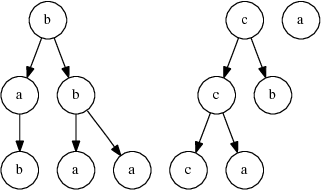
> DrawForest( Forest ) | ( function ) |
This will convert the forest Forest into a DOT graph file, run GraphViz on the resulting file and display the produced image in one of the PS viewer found on your system.
gap> DrawForest(f);
Displaying file: /tmp/tmp.2eSCn4/forest.dot.ps
|
1.2 Operations on forest algebras
Forest algebras are pairs (H,V) of monoids (horizontal and vertical) with a faithful monoidal action of V on H and a pair of morphism from H to V called the left and right insertions mathrmin_L and mathrmin_R such that mathrmin_L(g) * h=g+h and mathrmin_R(g)* h=h+g for all g,h in H. Forests algebras are created by giving the horizontal and vertical monoid, along with the action (the insertion functions are uniquely defined by the action and its axioms). The action table is only given for the generators of the vertical semigroup (recall that all semigroups in GAP are generated by some transformations).
1.2-1 ForestAlgebra
> ForestAlgebra( Horizontal, Vertical, Action ) | ( function ) |
Creates a forest algebra structure. Horizontal and Vertical are both in the Semigroup category, while Action is a matrix with m rows and n columns where m is the number of generators of Vertical and n is the number of elements in Horizontal. If E denotes the list of elements of Horizontal and G the list of generators of Vertical, Action[i][j]=k if and only if the action of G[i] on E[k] is E[k].
gap> H := Monoid([Transformation([2,2,3]), Transformation([3,3,3])]);
<monoid with 2 generators>
gap> V := Monoid([Transformation([2,2,3]), Transformation([3,3,3]),
Transformation([2,3,3])]);
<monoid with 3 generators>
gap> Elements(H);
[Transformation([1..3]), Transformation([2,2,3]), Transformation([3,3,3])]
gap> A := [[1, 2, 3 ],[2, 2, 3],[3, 3, 3],[2, 3, 3]];
gap> HV := ForestAlgebra(H, V, A);
<H has 3 generators and 3 elements, V has 4 generators>
|
1.2-2 Display
> Display( ForAlg ) | ( function ) |
Prints the multiplication table of the horizontal and vertical monoid, then the action table of ForestAlg.
gap> Display(HV);
[ [ 1, 2, 3 ],
[ 2, 2, 3 ],
[ 3, 3, 3 ] ]
[ [ 1, 2, 3, 4 ],
[ 2, 2, 4, 4 ],
[ 3, 3, 4, 4 ],
[ 4, 4, 4, 4 ] ]
[ [ 1, 2, 3 ],
[ 2, 2, 3 ],
[ 3, 3, 3 ],
[ 2, 3, 3 ] ]
|
1.2-3 ForestHorizontalMonoid
> ForestHorizontalMonoid( ForAlg ) | ( function ) |
Returns the horizontal monoid of ForestAlg.
gap> Elements(ForestHorizontalMonoid(HV));
[ Transformation( [ 1, 2, 3 ] ), Transformation( [ 2, 2, 3 ] ),
Transformation( [ 3, 3, 3 ] ) ]
gap> IsCommutative(ForestHorizontalMonoid(HV));
true
|
1.2-4 ForestVerticalMonoid
> ForestVerticalMonoid( ForAlg ) | ( function ) |
Returns the vertical monoid of ForestAlg.
gap> GreensJClasses(ForestVerticalMonoid(HV));
[{Transformation([3,3,3])},{Transformation([2,3,3])},
{Transformation([2,2,3])},{Transformation([1,2,3])}]
|
1.2-5 ForestAction
> ForestAction( ForAlg ) | ( function ) |
Returns the action table of ForestAlg.
1.2-6 ForestApplyAction
> ForestApplyAction( ForAlg, H, V ) | ( function ) |
Computes the action of V on H in ForestAlg. H can either be an element of the horizontal monoid of ForAlg (i.e. a transformation) or its index in the Elements of the horizontal monoid. V must be a transformation in the vertical monoid of ForAlg, this function finds a decomposition of V using generators of the vertical monoid and applies the action table on this decomposition.
gap> Elements(ForestVerticalMonoid(HV));
[Transformation([1,2,3]), Transformation([2,2,3]), Transformation([2,3,3]),
Transformation([3,3,3])]
gap> ForestApplyAction(HV, Transformation([1,2,3]), Transformation([2,3,3]));
Transformation([2,2,3])
|
1.2-7 IsHCommutative
> IsHCommutative( ForAlg ) | ( function ) |
> IsVCommutative( ForAlg ) | ( function ) |
Tests if the horizontal or vertical monoid of ForAlg is commutative.
1.2-8 IsHAperiodic
> IsHAperiodic( ForAlg ) | ( function ) |
> IsVAperiodic( ForAlg ) | ( function ) |
Tests if the horizontal or vertical monoid of ForAlg is aperiodic.
1.2-9 IsHIdempotent
> IsHIdempotent( ForAlg ) | ( function ) |
> IsVIdempotent( ForAlg ) | ( function ) |
Tests if the horizontal or vertical monoid of ForAlg is idempotent.
1.2-10 IsHRTrivial
> IsHRTrivial( ForAlg ) | ( function ) |
> IsVRTrivial( ForAlg ) | ( function ) |
Tests if the horizontal or vertical monoid of ForAlg is mathcalR-trivial.
1.2-11 IsHLTrivial
> IsHLTrivial( ForAlg ) | ( function ) |
> IsVLTrivial( ForAlg ) | ( function ) |
Tests if the horizontal or vertical monoid of ForAlg is mathcalL-trivial.
1.2-12 IsHJTrivial
> IsHJTrivial( ForAlg ) | ( function ) |
> IsVJTrivial( ForAlg ) | ( function ) |
Tests if the horizontal or vertical monoid of ForAlg is mathcalJ-trivial.
1.3 Operations on forest automata
A bottom-up deterministic forest automaton is a tuple (S, Q, s_0, A, gamma, lambda, F) where S is a finite set of horizontal states, s_0 in S is the initial state, F subseteq S is the set of accepting states, Q is a finite set of vertical states, gamma : S x Q -> S is a semiautomaton on set S with alphabet Q, A is the alphabet of input forests and lambda : S x A -> Q is the vertical output function.
1.3-1 ForestAutomaton
> ForestAutomaton( Det, S, Q, A, T, L, i, F ) | ( function ) |
Creates a forest automaton. Det is a boolean and must be set to true if the automaton is deterministic and false otherwise. If you input a non deterministic forest automatonm, it will be immediately transformed into an equivalent minimal deterministic automaton. S, Q and A are integers that denote respectively the number of horizontal and vertical states of the automaton and the size of the alphabet (notice that the set of horizontal states is then {1 dots S} and the set of vertical states is {1 dots Q}, the distinction between each kind of states is given by the context). T is a matrix with Q rows and S columns such that T[i][j]=k if and only if gamma(j, i)=k if the automaton is deterministic, of if gamma(j,i) in k otherwise. L is also a matrix with A rows and S columns such that L[i][j]=k if and only if lambda(j, a_i)=k if the automaton is deterministic, or if lambda(j, a_i) in k otherwise. i is the initial state (or set of initial states if the automaton is non deterministic). F is a list of accepting states.
gap> A := ForestAutomaton(true, 6, 3, 1,
[[2,5,6,6,6,6],[3,6,4,6,6,6],[6,6,6,6,6,6]],
[[1,3,3,1,2,3]],1,[2]);
<Forest automaton on {a}>
< deterministic automaton on 3 letters with 6 states >
gap> B := ForestAutomaton(true, 4, 4, 2,
[[3,3,3,4],[2,2,3,4],[1,1,3,4],[4,4,4,4]],
[[1,1,4,4],[2,3,1,4]],1,[1,2,3]);
<Forest automaton on {ab}>
< deterministic automaton on 4 letters with 4 states >
gap> C := ForestAutomaton(true, 3, 3, 2,
[[1,2,3],[2,2,3],[3,3,3]], [[2,3,3],[1,2,3]],1,[1,2]);
<Forest automaton on {ab}>
< deterministic automaton on 3 letters with 3 states >
gap> ND := ForestAutomaton(false, 4, 2, 2,
[[[1,2],,4,],[1,3,,]], [[1,,1,],[2,2,,]],1,[4]);
<Forest automaton on {ab}>
< deterministic automaton on 3 letters with 5 states >
|
1.3-2 Display
> Display( ForAut ) | ( function ) |
Displays the transition table of ForAut, its initial and accepting states and output function.
gap> Display(A);
| 1 2 3 4 5 6
-----------------------
1 | 2 5 6 6 6 6
2 | 3 6 4 6 6 6
3 | 6 6 6 6 6 6
Initial state: [ 1 ]
Accepting state: [ 2 ]
Output function :
[ [ 1, 3, 3, 1, 2, 3 ] ]
|
1.3-3 TreesForestAutomaton
> TreesForestAutomaton( n ) | ( function ) |
Returns the minimal automaton that recognizes the language of all trees on an alphabet with n letters.
gap> TreesForestAutomaton(4);
<Forest automaton on {abcd}>
< deterministic automaton on 1 letters with 3 states >
|
1.3-4 ReachableStatesForestAutomaton
> ReachableStatesForestAutomaton( A ) | ( function ) |
Trims A of its non reachable states. This function is automatically called after determinization or before minimization.
1.3-5 ProductForestAutomaton
> ProductForestAutomaton( A1, A2, F ) | ( function ) |
Given two forest automata A1 and A2 on the same alphabet, computes the product automaton of A1 and A2 using F as the set of accepting states. F must be a list of products of states from A1 and A2, e.g. [[1,3], [2,5]...]. This function mainly exists to provide the union and intersection operators. The resulting automaton is trimmed but not minimized; it is not minimal in general.
1.3-6 ComplementForestAutomaton
> ComplementForestAutomaton( A ) | ( function ) |
Given a forest automaton A complement the set of accepting state of A. This function returns the complemented automaton but be aware that it also alters the original automaton A. If you want to preserve A use -A instead.
1.3-7 \*
> \*( A1, A2 ) | ( function ) |
Returns the minimal automaton that recognizes the intersection of the languages accepted by A1 and A2. The resulting automaton is trimmed but not minimized; it is not minimal in general.
gap> A*TreesForestAutomaton(1);
<Forest automaton on {a}>
< deterministic automaton on 3 letters with 6 states >
|
1.3-8 \+
> \+( A1, A2 ) | ( function ) |
Returns the minimal automaton that recognizes the union of the languages accepted by A1 and A2. The resulting automaton is trimmed but not minimized; it is not minimal in general.
gap> B+C;
<Forest automaton on {ab}>
< deterministic automaton on 3 letters with 3 states >
|
1.3-9 \-
Returns A with the set of accepting states complemented. Unlike ComplementForestAutomaton this does not alter A but the returned automaton shares the same transition table and output function in memory.
1.3-10 ForestAutomatonAccepts
> ForestAutomatonAccepts( ForAut, For ) | ( function ) |
Returns true if ForAut accepts the forest For and false otherwise.
gap> f := Forest("a(a(a+a)+a(a(a(a+a)+a(a+a))+a))");
a(a(a+a)+a(a(a(a+a)+a(a+a))+a))
gap> ForestAutomatonAccepts(A, f);
true
|
1.3-11 MinimalForestAutomaton
> MinimalForestAutomaton( ForAut ) | ( function ) |
Computes the minimal forest automaton of ForAut. It is safe to call this function multiple times on the same automaton as it stores the result of its computation. This function does not change the name of states for automaton that are already reduced.
gap> MinimalForestAutomaton(B);
<Forest automaton on {ab}>< deterministic automaton on 3 letters with 3 states >
gap> B;
<Forest automaton on {ab}>< deterministic automaton on 4 letters with 4 states >
|
1.3-12 TransitionForestAlgebra
> TransitionForestAlgebra( ForAut ) | ( function ) |
Returns the transition forest algebra of ForAut.
gap> HV := TransitionForestAlgebra(A);
<H has 3 generators and 5 elements, V has 4 generators>
gap> IsHAperiodic(HV);
true
|
1.3-13 SyntacticForestAlgebra
> SyntacticForestAlgebra( ForAut ) | ( function ) |
Minimizes ForAut and returns its transition forest algebra, i.e. the syntactic forest algebra of the language recognized by ForAut.
gap> HV := SyntacticForestAlgebra(B);
<H has 4 generators and 4 elements, V has 7 generators>
gap> IsHCommutative(HV);
false
|
1.3-14 HorizontalForestAutomaton
> HorizontalForestAutomaton( ForAut ) | ( function ) |
Returns an Automaton object (as used by the automata package) describing the horizontal automaton of ForAut, i.e. the automaton (S, Q, gamma, s_0, F).
gap> ForestHorizontalAutomaton(C);
< deterministic automaton on 3 letters with 3 states >
|
1.3-15 ExistsPathInLanguageAutomaton
> ExistsPathInLanguageAutomaton( Regular, Maximal ) | ( function ) |
Regular can either be an automaton or a rational expression describing a regular language L. Computes a forest automaton that accepts forests containing a path labelled with a word in L. Maximal is a boolean, if true such a path must be maximal, it can be any path otherwise. The labelling of a path is read from the root to the leaves. Because the resulting automaton can be huge, it is trimmed but not minimized.
gap> AB := RationalExpression("ab");
ab
gap> Aab := ExistsPathInLanguageAutomaton(AB, false);
<Forest automaton on {ab}>
< deterministic automaton on 3 letters with 4 states >
gap> ForestAutomatonAccepts(Aab, Forest("ba"));
true
gap> ForestAutomatonAccepts(Aab, Forest("bab"));
true
gap> Aabmax := ExistsPathInLanguageAutomaton(AB, true);
<Forest automaton on {ab}>
< deterministic automaton on 3 letters with 5 states >
gap> ForestAutomatonAccepts(Aabmax, Forest("bab"));
false
|
1.3-16 WriteDotForestAutomaton
> WriteDotForestAutomaton( ForAut, File ) | ( function ) |
Creates a GraphViz Dot file describing the automaton ForAut. The ouput in written in File in a temporary directory. This function returns the directory where File was written.
gap> WriteDotForestAutomaton(A, "automaton_1");
dir("/tmp/tmp.0YxjY3/")
|
1.3-17 DrawForestAutomaton
> DrawForestAutomaton( ForAut ) | ( function ) |
Uses GraphViz to draw the automaton ForAut and displays the resulting postscript file.
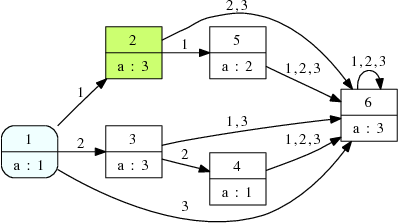
gap> DrawForestAutomaton(A);
Displaying file: /tmp/tmp.sX024c/forest_automaton.dot.ps
|
1.3-18 WriteDotForestAction
> WriteDotForestAction( ForAut, File[, IgnElts] ) | ( function ) |
This function computes the horizontal transformation monoid of ForAut and how the left and right insertions and rootings act on its elements. The ouput is a GraphViz Dot file written in File. This function accepts an optional argument IgnElts; it can either be a integer or a list or integers that correspond to elements of the horizontal transformation monoid (using the order given by the Elements function) to be ignored, for instance those corresponding to sink states. This function returns the temporary directory where File was written. Important remark: this function does not minimize the automaton
gap> WriteDotForestAction(A, "action_1");
dir("/tmp/tmp.0YxjY3/")
|
1.3-19 DrawForestAutomatonAction
> DrawForestAutomatonAction( ForAut[, IgnElts] ) | ( function ) |
Similar to WriteDotForestAction, but draws a postscript file of the graph and displays it.

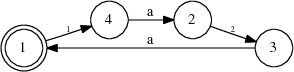

gap> DrawForestAutomatonAction(A);
gap> DrawForestAutomatonAction(A, 5);
gap> DrawForestAutomatonAction(B, 4);
|
1.4 WS2S: monadic second order logic on forests
It is well known that the class of recognizable forests is equal to the class of forest languages that can be defined by a monadic second order logic sentence using two predicates for next child and parent. This set of functions allows you to compile a MSO sentence into a deterministic forest automaton. Although each quantifier can potentially cause an exponential blowup in the number of states the use of an efficient determinization and minimization algorithm allows to compile most sentences in a reasonable amount of time, provided you make sure to use quantifiers in the smallest possible scope, in particular you should not try to write all the quantifiers in front of the formula.
1.4-1 MSOSentence
> MSOSentence( S ) | ( function ) |
This is the parser of MSO sentences, using the following grammar:
F ::= @X F / &X F / !x F / ?x F / x.a / x<y / x<=y /
x<<y / x|y / x||y / x-y / ^x / $x / #X / x=y / F+F / F*F / F=>F / ~F
First order variables are denoted by lower case letters x, y, z ... Second order variables are denoted by upper case letters X, Y, Z ... The universal and existential quantifiers for second order variables are denoted respectively @ and & while their first-order counterparts are denoted ! and ?. In a MSO formula, first order variables denote nodes in the forest, while second order variables denote finite sets of nodes. x<y (x<=y) means y is the next sibling (or y=x), while x-y means y is any right sibling of x. x|y and x||y respectively mean that x is the parent (an ancestor) of y. Finally, << is the order on nodes of a forest given by a depth-first searh. x.a means that the label of the node x is a. ^x and $x are used respectively to denote that x is a root and a leaf. Note that in forests there can be several roots and some of them can also be leaves. #X is true if X denotes a maximal path of the forest. Negation of a formula is denoted ~F, while conjunction and disjunction are denoted respectively F+F and F*F. Because the parsing capabilities of GAP are limited, the precedence of some operators might not be what you expect. Always add parentheses when in doubt ; after the sentence is parsed it will be printed with all implicit parentheses added to make sure the formula is correct. All spaces are ignored inside a formula.
gap> R := MSOSentence("!x x.a=>$x");
!x (x.a)=>($x)
gap> S := MSOSentence("!x x.b => (^x + ?y y.a * y|x)");
!x (x.b)=>((^x)+(?y (y.a)*(y|x)))
gap> T := MSOSentence("&X #X*(!x x:X => (^x + (?y y:X*y|x* (x.a=>y.b) * (x.b=>y.a))))");
&X (#X)*(!x (x:X)=>((^x)+(?y (y:X)*((y|x)*(((x.a)=>(y.b))*((x.b)=>(y.a)))))))
# Even number of a's in the whole forest
gap> U := MSOSentence(Concatenation(
"&X &Y (!x (x.a)=>(((x:X)*(~(x:Y)))+((x:Y)*(~(x:X)))))",
"*((!x ((x:X)+(x:Y))=>(x.a))*((!x ((x.a)*(!y y.a=>~(y<<x)))=>(x:X))",
"*((!x (x:X)=>(?y (y:Y)*((x<<y)*(!z (z.a)=>(~((x<<z)*(z<<y)))))))",
"*(!y (y:Y)=>((?x (x:X)*((y<<x)*(!z (z.a)=>(~((y<<z)*(z<<x))))))",
" +(!x (x.a)=>(~(y<<x))))))))"));
|
1.4-2 MSOForestAutomaton
> MSOForestAutomaton( S, n ) | ( function ) |
Compiles the given (parsed) MSO sentence into a forest automaton accepting the language defined by S. n is an optional parameter to specify the size of the alphabet. If it is omitted all letters that appear in the formula will be used as the alphabet.
gap> A := MSOForestAutomaton(R, 3);
<Forest automaton on {abc}>< deterministic automaton on 3 letters with 3 states >
gap> B := MSOForestAutomaton(S, 4);
<Forest automaton on {abcd}>< deterministic automaton on 3 letters with 3 states >
gap> C := MSOForestAutomaton(T);
<Forest automaton on {ab}>< deterministic automaton on 2 letters with 3 states >
gap> D := MSOForestAutomaton(U,3);
<Forest automaton on {abc}>< deterministic automaton on 2 letters with 2 states >
|





